จำนวนจริง

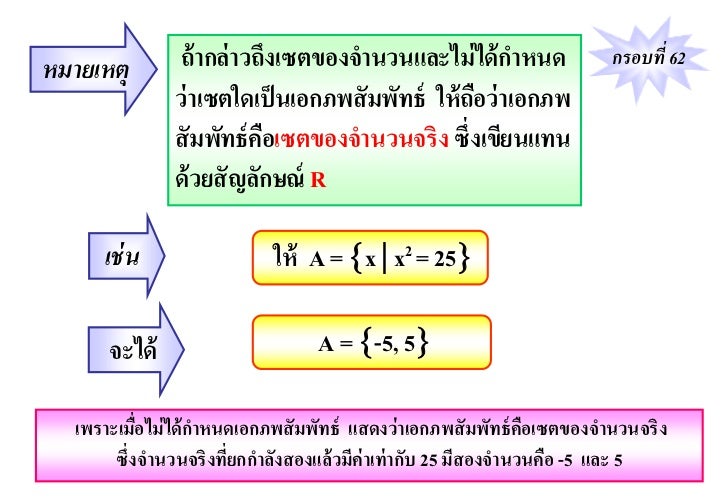
มีหลักเกณฑ์ในการแบ่งจำนวนจริงอยู่หลายเกณฑ์ เช่น จำนวนตรรกยะ หรือ จำนวนอตรรกยะ; จำนวนพีชคณิต (algebraic number) หรือ จำนวนอดิศัย; และ จำนวนบวก จำนวนลบ หรือ ศูนย์

จำนวนจริงแทนปริมาณที่ต่อเนื่องกัน โดยทฤษฎีอาจแทนได้ด้วยทศนิยมไม่รู้จบ และมักจะเขียนในรูปเช่น 324.823211247… จุดสามจุด ระบุว่ายังมีหลักต่อ ๆ ไปอีก ไม่ว่าจะยาวเพียงใดก็ตาม

การวัดในวิทยาศาสตร์กายภาพเกือบทั้งหมดจะเป็นการประมาณค่าสู่จำนวนจริง การเขียนในรูปทศนิยม (ซึ่งเป็นจำนวนตรรกยะที่สามารถเขียนเป็นอัตราส่วนที่มีตัวส่วนชัดเจน) ไม่เพียงแต่ทำให้กระชับ แต่ยังทำให้สามารถเข้าใจถึงจำนวนจริงที่แทนได้ในระดับหนึ่งอีกด้วย อ่านเพิ่มเติม

การให้เหตุผลแบบนิรนัย

การให้เหตุผลแบบนิรนัย

                การให้เหตุผลแบบนิรนัยเป็นวิธีการให้เหตุผลโดยสรุปผลจากข้อความซึ่งเป็นความจริงทั่วไปมาเป็นข้ออ้างเพื่อสนับสนุนให้เกิดข้อสรุปที่เป็นความรู้ใหม่ที่เป็นข้อสรุปส่วนย่อยข้อสรุปที่ได้จากการให้เหตุผล อ่านมมเพิ่มเติม

การให้เหตุผลแบบอุปนัย

การให้เหตุผลแบบอุปนัย
การให้เหตุผลแบบอุปนัย (Inductive Reasoning) เกิดจากการที่มีสมมติฐานกรณีเฉพาะ หรือเหตุย่อยหลายๆ เหตุ เหตุย่อยแต่ละเหตุเป็นอิสระจากกัน มีความสำคัญเท่าๆ กัน และเหตุทั้งหลายเหล่านี้ไม่มีเหตุใดเหตุหนึ่งแสดงให้เห็นถึงความเป็นสมมติฐานกรณีทั่วไป หรือกล่าวได้ว่า การให้เหตุผลแบบอุปนัยคือการนำเหตุย่อยๆ อ่านเพิ่มเติม 

ยูเนี่ยน อินเตอร์เซกชันและคอมพลีเมนต์ของเซต

ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออยเลอร์ เราลองมาดูกันครับว่ายูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นอย่างไรพร้อมตัวอย่าง อ่านเพิ่มเติม

สับเซตและเพาเวอร์เซต

สับเซตและเพาเวอร์เซต

• สับเซต
บทนิยาม เซต A เป็นสับเซตของเซต B ก็ต่อเมื่อ สมาชิกทุกตัวของเซต A เป็นสมาชิกของเซต B และสามารถเขียนแทนได้ด้วยสัญลักษณ์ A ⊂B
ตัวอย่างที่ 1 A = {1, 2, 3}
B = { 1, 2, 3, 4, 5}
∴ A ⊂ B เพิ่มเติม

เอกภพสัมพันธ์

เอกภพสัมพัทธ์

เอกภพสัมพัทธ์ คือ เซตที่ถูกกำหนดขึ้นโดยมีข้อตกลงว่า จะกล่าวถึงสิ่งที่เป็นสมาชิกของเซตนี้เท่านั้น จะไม่กล่าวถึงสิ่งอื่นใดที่ไม่เป็นสมาชิกของเซตนี้ โดยทั่วไปจะใช้สัญลักษณ์ แทนเซตที่เป็นเอกภพสัมพัทธ์ อ่านเพิ่มเติม

เซต

เซต (อังกฤษ: set) ในทางคณิตศาสตร์นั้น อาจมองได้ว่าเป็นการรวบรวมกลุ่มวัตถุต่างๆ ไว้รวมกันทั้งชุด แม้ว่าความคิดนี้จะดูง่ายๆ แต่เซตเป็นแนวคิดที่เป็นรากฐานสำคัญที่สุดอย่างหนึ่งของคณิตศาสตร์สมัยใหม่ การศึกษาโครงสร้างเซตที่เป็นไปได้  อ่านเพิ่มเติม